Rederive

Preamble

This article establishes one of the foundations of physics: Vectors. Vectors in physics are used a little differently than in math (at least at high school level), and so this article is tailored to physics only.

Need for Directions

In physics, some quantities exist that need to be described by more than just their magnitude (number value). Why? Because to their values behave differently based on which direction they are pointing towards. Think back to relative velocity; When the trains were moving in the same direction, you could see the other train move slowly or even stay still (if both trains have same speed). Now, imagine the trains have the same speed but the other train is moving in the opposite direction. You will see that not only is it moving away, its moving away much faster than its speed would say. In both cases the speed of the trains are the same, yet their effects are altered due to the direction of these trains.

Finally: What if the train parts ways with you while going in the same direction? How fast would it seem to be going away then?

If you imagine that someone is pushing the trains away, then you must consider how strong of a force they are applying. But if you think about it, the scenario is similar in its result. So, force also requires a direction to use fully.

What else? Try to imagine quantities you already know which require directions. Displacement! Of course, velocity is measured using displacement and not distance, meaning displacement is also a directed measurement.

Other directed quantities would be momentum, acceleration, electric field, magnetic field, etc. (more on these later).

Vector Representation

Let us just oversee how to describe a vector. If a quantity X is a vector. We show it by writing it in bold X or with an arrow on top;

So obviously, for a vector quantity we should have more than one direction. Let’s consider that we are looking at our scenario from above (maybe you’re a God). Then, we would just be able to see objects move left, right, up, or down. For us, the system is 2-dimensional.
On the graph, we will draw the vector as an arrow that points in the vector’s direction. To show the magnitude of the vector (how fast the train is, how strong you are pushing, etc.), we will make the arrow as long (for higher value) or short (for lower value) as needed.

Let’s say that a train (T1) starts from a station, which is located at origin (0,0).

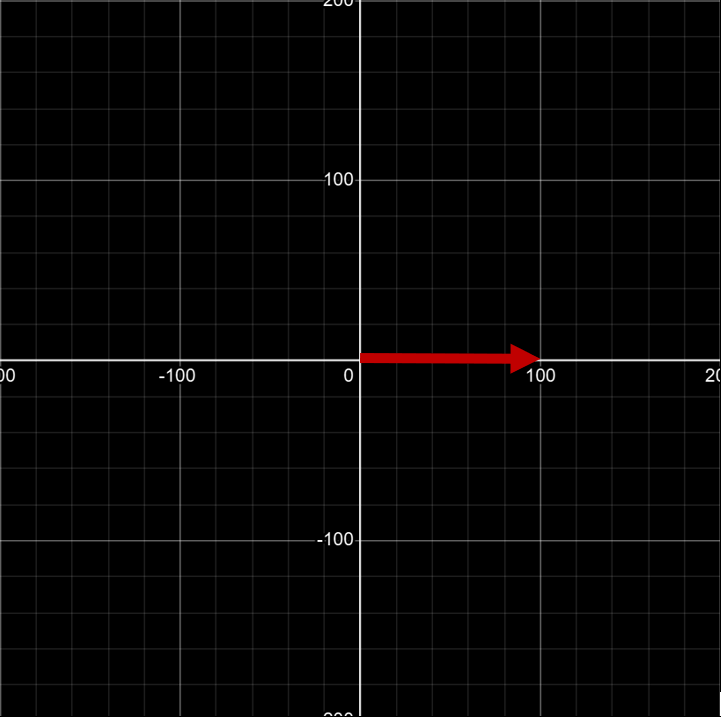
Now, take three more trains: T2 moves in the same direction as the first but with velocity 200 km/h , while T3 moves straight up (on the y-axis), and T4 moves in the opposite direction (x-axis in the left direction). Let’s say T3, T4 move with a speed of 100km/h as well. We say that T1 is moving in the +x direction, T3 is moving in +y direction, and T4 is moving in -x direction.

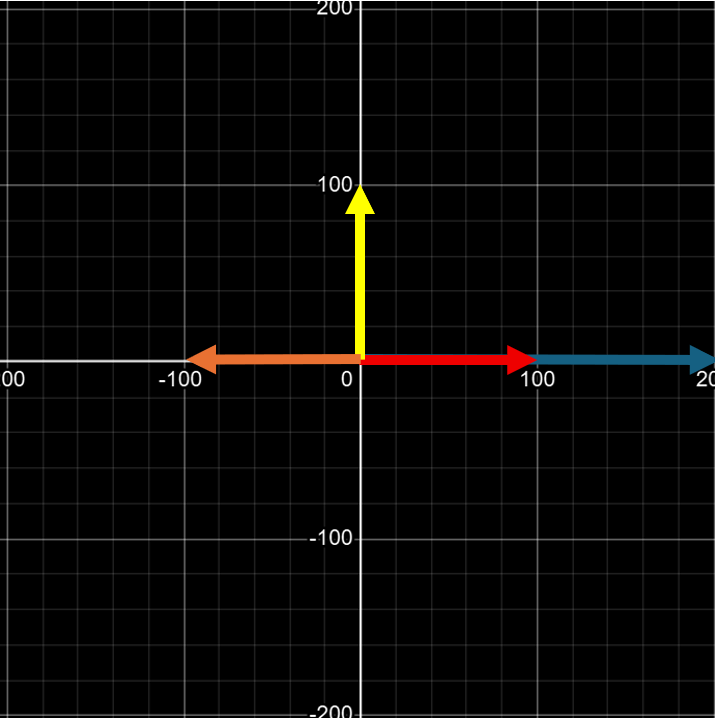
Constancy

One last thing to understand, is that a vector by definition is complete when it has a magnitude and a direction. This means that a vector does not need a position to be defined, i.e. a vector will stay the same no matter where you put it, as long as the length and direction are unchanged.

For example, pushing a desk to the right, as long as the force applied and direction are same and on the same side of the desk, the force vector is unchanged no matter which point on that side you push from.

Conclusion

Next, we will go over the algebra of vectors, using more diagrams. For physics, we will understand this algebra through examples of physical quantities such as displacement, velocity, acceleration, etc.